Introduction Link to heading
We run a preorder depth first search on the root of a binary tree.
At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node. (If the depth of a node is D, the depth of its immediate child is D+1. The depth of the root node is 0.)
If a node has only one child, that child is guaranteed to be the left child.
Given the output S of this traversal, recover the tree and return its root.
Example 1:
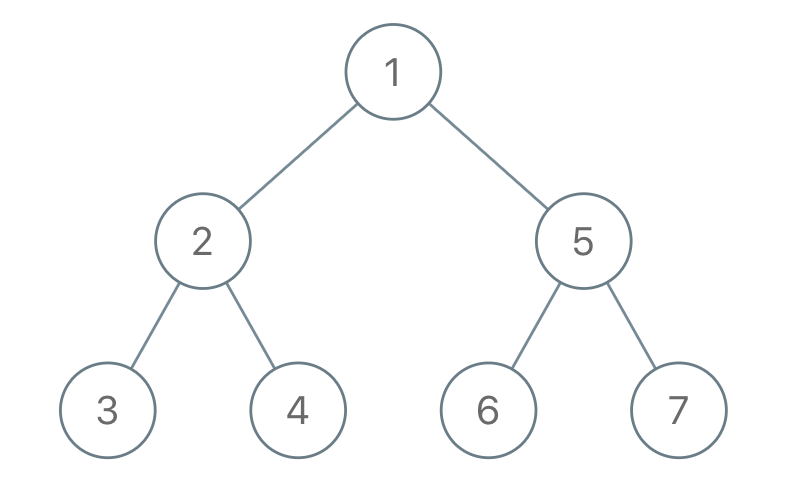
Input: "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]
Example 2:
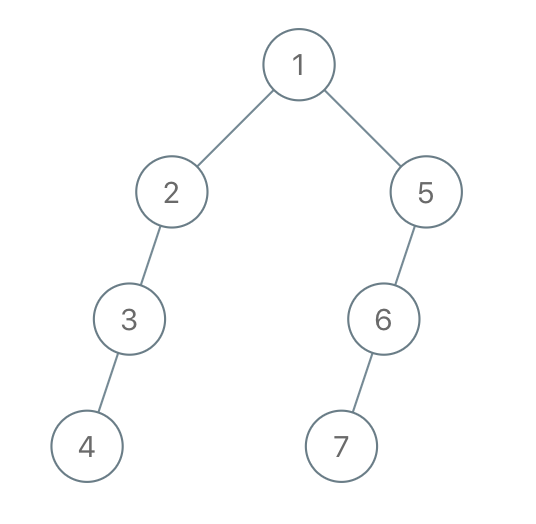
Input: "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]
Example 3:
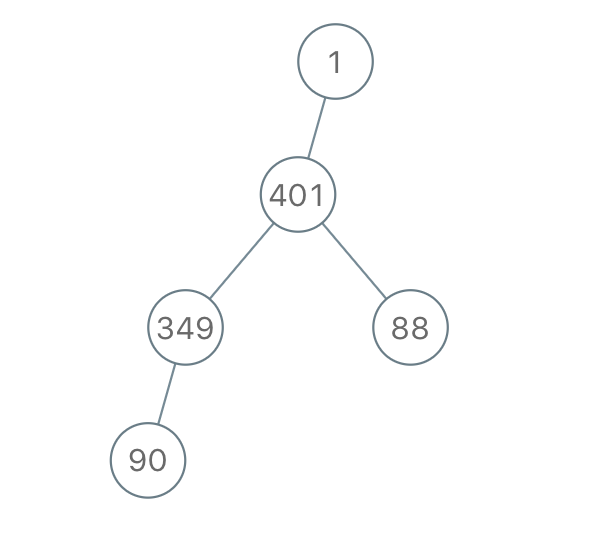
Input: "1-401--349---90--88"
Output: [1,401,null,349,88,90]
Note:
The number of nodes in the original tree is between 1 and 1000.
Each node will have a value between 1 and 10^9.
Solution Link to heading
DFS (Deep First Search) solution:
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func recoverFromPreorder(S string) *TreeNode {
root, _ := recoverR(S, 0)
return root
}
func recoverR(S string, level int) (*TreeNode, string) {
l, s := readDepth(S)
if l != level {
return nil, S
}
val, s := readValue(s)
root := &TreeNode{val, nil, nil}
root.Left, s = recoverR(s, level+1)
root.Right, s = recoverR(s, level+1)
return root, s
}
func readValue(S string) (int, string) {
n := len(S)
for i := 0; i < n; i++ {
ch := S[i]
if ch == '-' {
v, _ := strconv.Atoi(S[:i])
return v, S[i:]
}
}
v, _ := strconv.Atoi(S)
return v, ""
}
func readDepth(S string) (int, string) {
n := len(S)
for i := 0; i < n; i++ {
ch := S[i]
if ch != '-' {
return i, S[i:]
}
}
return -1, ""
}
Explanation Link to heading
We need to implement readers first readDepth and readValue. When readers are implemented we can traverse the tree by using DFS recursive algorithm that will check level on each step and build nodes.