Introduction Link to heading
We write the integers of A and B (in the order they are given) on two separate horizontal lines.
Now, we may draw a straight line connecting two numbers A[i] and B[j] as long as A[i] == B[j], and the line we draw does not intersect any other connecting (non-horizontal) line.
Return the maximum number of connecting lines we can draw in this way.
Example 1:
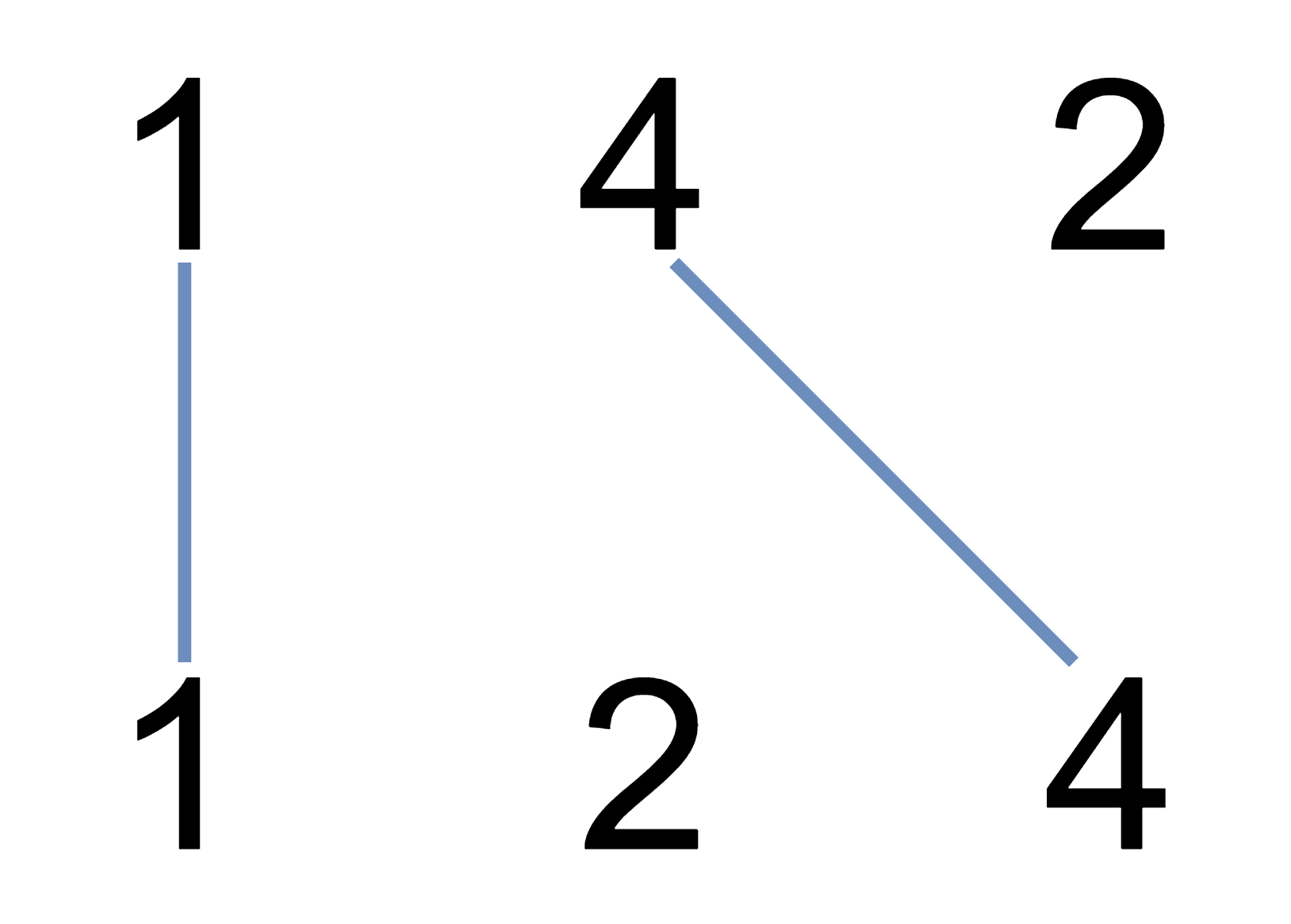
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.
Example 2:
Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3
Example 3:
Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2
Note:
1 <= A.length <= 500
1 <= B.length <= 500
1 <= A[i], B[i] <= 2000
Solution Link to heading
Dynamic programming solution:
func maxUncrossedLines(A []int, B []int) int {
n := len(A)
m := len(B)
dp := make([][]int, n+1)
dp[0] = make([]int, m+1)
for i := 1; i <= n; i++ {
dp[i] = make([]int, m+1)
for j := 1; j <= m; j++ {
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
if A[i-1] == B[j-1] {
dp[i][j] = max(dp[i][j], dp[i-1][j-1]+1)
}
}
}
return dp[n][m]
}
func max(a, b int) int {
if a >= b {
return a
} else {
return b
}
}
Explanation Link to heading
This problem could be transformed in to “Find the longest subsequence that exist in another array”. Based on that, the best solution could be in Dynamic Programming, because other solutions will work too long.
In other to solve DP problem we need to find a sub-problem. Our sub-problem is to find similarity of two arrays, that is related to “Edit Distance”.
We would need 2D matrix, each cell is the max subsequence value of two sub-problems A[0:i] and B[:j].